Remark on applications of Tseng und Husing to boolean equations and graph theoretic problem
Remark on applications of Tseng und Husing to boolean equations and graph theoretic problem
For further information, please see https://zhuanlan.zhihu.com/p/575591863
Consider a boolean system $x_1(t+1)=f(x_1(t),x_2(t),\cdots,x_n(t)),x_2(t+1)=f(x_1(t),\cdots,x_n(t)),\cdots,x_n(t+1)=f(x_1(t),\cdots,x_n(t))$,in which $x_i(t)$ represents the value that the valuation $t$ assigns to $x_i$.
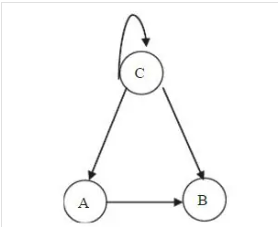
e.g. $x_1(t+1)=\lnot x_3(t),x_2(t+1)=x_1(t)\lor x_3(t),x_3(t+1)=x_3(t)$.
 ,
,
For a boolean system, if for a valuation $t$, $x_i(t+n)=x_i(t)$, then $n$ is a period $x_i$. The periods of the boolean equations are the periods of $x_1,\cdots,x_n$. A period $p$ is said to be primary, if $p$ is not divisible by $m$ for any period $m$ of the boolean equations with $m \not= p$.
A result of Tseng und Husing is, for any boolean equations with $n$ variables $x_1,x_2,\cdots,x_n$, we can construct a system of boolean equations with $mn$ variables s.t. for any $x_i$, the value of $x_i$ does not depend on its value in the previous stage,and the set of primary periods of the system of boolean equation is the same as the former.
Boolean network has been used in biology, e.g. NK model.
Boolean systems can be used to represent circuits, in which the value of $x_i$ (0 or 1) represents the state of $x_i$ (off or on). Thus the above result can be seen as a result saying that for any boolean circuit, we can construct a boolean circuit s.t. for any $x_i$ in the circut, the state of $x_i$ does not depend on its state in the previous stage, and the ways of change of the states of the later boolean circuit is similar to the former.
We can use another way, a “graph-theoretic” way, to describe this topic.
The question is about how to arrange 8 girls into two groups such that each group consists of at least two girls, and for each group, the girls in it must satisfy the following condtions: (1) every girl puts her hands on someone else’s shoulders; (2) either (i) every girl’s shoulders are put hands by someone else (and only by that one), or (ii) every girl except one’s shoulders are put hands by someone else, but at the same time there is only one girl whose shoulders are put hands by two different girls. We can use graph to represent the relations between girls. We use points to stand for girls. Whenever a girl puts her hands on another’s shoulders, we draw a arrow from the former to the latter.
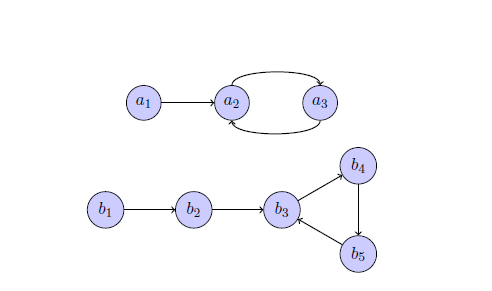
For example, the girls are arranged into two groups. In one group, girl a1 puts her hands on a2’s shoulders, a2 and a3 put theirs hands on each other’s shoulders (and so the two girls have to stand face to face). We will say that there is a 2-circle in such a group. In the other group, there is a 3-circle: girl b3 puts their hands on b4’s shoulders, b4 puts their hands on b5’s shoulder, and b5 puts their hands on b3’s shoulder (sorry for that two of them may have to turn sideways so as to put their hands on the shoulders of the girls standing in front of them). Notice that in such an arrangement, both groups satisfy requirement (2)-(ii). We will only consider those arrangements in each group of which there is a (unque) circle. Let call the above arrangement has the (2, 3)-circle.
Now to raise the quesiton, we will consider one more condition which is related the colors of the girls’ wearings. We suppose the 8 girls wear a hat (either black or white), a skirt (either red or green), and a pair of shoes (either pink or orange). The additional condition (called ‘the 3-wearing condition’) is as follows:
a. Each girl dresses differently from the others (there are 2^3=8 ways of dressing with 3 items of clothing);
b. For any two girls a and a′, if two of their wearings have the same color respectively (for example, their hats are both white and their skirt are both red), the two girls whose shoulders a and a′ put theirs hands on must have the third wearing of the same color (correspondingly, the shoes of the two girls must be of the same color).
Question: Is there a (2, 3)-circle arrangement for 8 girls such that the 3-wearing condition is satisfied? If the answer to the above question is negative, we will ask the similar question for 16 girls except that we will consider one more wearing, for instance, the socks (either coffee or wine), and correspondingly the 4-wearing requirement is that for any two girls a and b, if three of their wearings have the same color respectively, the two girls whose shoulders a and b put theirs hands on must have the fourth wearing of the same color. Furthermore, for the case of 16 girls, we would like to ask whether there is a (2, 3, 5)-circle arrangement satisfying the 4-wearing condition. Notice, in such arrangement, the girls are arranged into three groups, in which there are a 2-circle, a 3-circle and a 5-circle respectively. How about a (3, 4, 5)-circle arrangement? A (2, 3, 7)-circle arrangement? and so on. At last, we certainly can ask the similar questions for 2^n girls of n different wearings for any n ≥ 3.
详情请见:https://zhuanlan.zhihu.com/p/575591863
考虑布尔方程组$x_1(t+1)=f(x_1(t),x_2(t),\cdots,x_n(t)),x_2(t+1)=f(x_1(t),\cdots,x_n(t)),\cdots,x_n(t+1)=f(x_1(t),\cdots,x_n(t))$,其中$x_i(t)$代表$x_i$在赋值$t$下的值, 取值为$0,1$, $f$为一真值函数.
如$x_1(t+1)=\lnot x_3(t),x_2(t+1)=x_1(t)\lor x_3(t),x_3(t+1)=x_3(t)$.
其可用图1表示,
 ,
,
即下一阶段$x_1$的值为$1$当且仅当此一阶段$x_3$的值为$0$, 下一阶段$x_2$的值为$1$,当且仅当此一阶段$x_1$或$x_3$的值为$1$,$\ldots$.
我们可以看出,下一阶段$x_i$的值完全由此一阶段$x_1,\cdots,x_n$的真值决定,这也是我们为什么叫$f$真值函数的原因.
我们如下定义布尔方程的主周期:某布尔方程组,若对某赋值$t$, $x_i(t+n)=x_i(t)$,我们称$n$为$x_i$的一个周期.布尔方程组的周期集为为$x_1,\cdots,x_n$的周期.而一个周期被称为主周期当且仅当它不为该方程组的任何其它周期整除.
Tseng und Husing的一个结果是:对于任何一个有$n$个变量$x_1,x_2,\cdots,x_n$布尔方程组,我们都可以构造出一个有$mn$个变量的布尔方程组使得在后者,对于任何$x_i$,其值都并不依赖于上一阶段$x_i$的值,并且其主周期和前面的布尔方程组一样.
布尔网络已经用于生物学中,例如NK模型。
我们可以看出,布尔方程可以用来表示电路,其中$x_i$的值$0,1$可以用来表示$x_i$在该阶段是激活还是关闭.因此,上面的结果可以看作对于某一布尔电路,我们都可以构造出另一个布尔电路, 使得其中所有机关都并不依赖自身在上一阶段的值,而变换方式仍大体与前者相同.
而我们也可以换一种方式,用“图论”来描述这个话题.
问题是关于如何将8个女孩分成两组,使每组至少由两个女孩组成,对于每组,其中的女孩必须满足以下条件。 (1) 每个女孩都把她的手放在别人的肩上。 (2)要么(i)每个女孩的肩膀都被别人搭上(而且只被那个女孩搭上),要么(ii)除了一个女孩的肩膀外,每个女孩都被别人搭上,但同时只有一个女孩的肩膀被两个不同的女孩搭上。 我们可以用图来表示女孩之间的关系。我们用点来代表女孩。每当一个女孩把她的手放在另一个女孩的肩膀上,我们就画一个从前者到后者的箭头。
例如,女孩们被安排成两组。在一组中,女孩a1将她的手放在a2的肩膀上,a2和a3将她们的手放在互相的肩膀上。这样我们就说,在这样一组中存在一个2循环。在另一组中则有一个3循环:女孩b3把她们的手放在b4的肩膀上,b4把她们的手放在b5的肩膀上,b5把她们的手放在b3的肩膀上。在这样的安排中,两组都满足要求(2)(ii)。让我们把上述安排称为有一个(2,3)循环。

我们还要考虑一个条件。我们假设8个女孩都戴着一顶帽子(黑色或白色),一条裙子(红色或绿色),一双鞋(粉色或橙色)。附加条件如下。
a. 每个女孩都与其她女孩的穿着方式不同(3件穿着,有2^3=8种组合方式);
b. 对于任何两个女孩a和b,如果她们的两件衣服分别具有相同的颜色(例如,她们的帽子都是白色的,裙子都是红色的),那么a和b把手放在肩膀上的另外两个女孩的第三件穿戴的颜色必须相同(相应地,两个女孩的鞋子必须是相同颜色的)。
问题:是否有一个8个女孩的(2,3)循环的安排,使上述附加条件得到满足? 如果上述问题的答案是否定的,我们将对16个女孩的情况提出类似的问题,只是我们将让她们多穿一件,例如袜子(褐色或紫色),并且相应地:对于任何两个女孩a和b,如果她们有任意三件穿戴分别具有相同的颜色,那么a和b把手放在肩膀上的另外两个女孩的第四件穿戴的颜色必须相同。 此外,对于16个女孩的情况,我们想问是否有一个(2,3,5)循环安排,满足以上条件。注意,在这样的安排中,女孩们被安排成三组,其中分别有一个2循环、一个3循环和一个5循环。类似的,(3,4,5)循环的安排呢?一个(2,3,7)-循环的排列呢? 等等。 最后,我们当然可以对任何n≥3的有n件不同穿戴的2^n个女孩提出类似问题。
Reference
Zeng und Hsiung, An Approach to Boolean Paradoxes of Indirect Self-Reference, forthcoming.